推荐阅读

  1. 机器学习笔记10——EM算法原理与详细推导 | issey的博客
  2. 机器学习笔记11——【GMM 1】高斯混合模型原理与推导 | issey的博客

前言

前几天忙着开学的事，加上图像处理的学习，这篇文章稍微搁置了些时间。闲话不多说，直接进入正题。本篇对EM算法和高斯混合模型的推导过程不会再详细说明，相关部分请见前两篇文章。

高斯混合模型的聚类步骤

回顾在上一篇文章结尾，GMM聚类步骤为：

step1：

定义高斯分布个数K，对每个高斯分布设置初始参数值\(\theta^{(0)}_k = \alpha_k,\mu_k,\Sigma_k\) 。一般第一步不会自己设置初始值，而是通过K-mean算法计算初始值。

step2 E-step：

根据当前的参数\(\theta^{(t)}\) ,计算每一个隐变量的后验概率分布\(\gamma_t(z^{(i)})\)。精确到每一个后验概率的计算，有

\[ \gamma_t(z_k^{(i)}) = \frac{\alpha_k^{(t)}N(x|\mu_k^{(t)},\Sigma_k^{(t)})}{\sum_{j=1}^K \alpha_j^{(t)}N(x|\mu_j^{(t)},\Sigma_j^{(t)})} \]

这里解释一下：

  • \(\gamma_t(z_k^{(i)})\) ：在第t轮时，第i个样本的隐变量z的第k个概率。或者说，在第t轮时，第i个样本属于第k个高斯分布的后验概率。
  • \(\alpha_k^{(t)}\)：在第t轮时，已固定的第k个高斯分布的权值。
  • \(N(x|\mu_k^{(t)},\Sigma_k^{(t)})\) ：在第t轮时，第k个已固定的多维高斯分布概率密度函数。
  • 带上标(t)的都是已固定参数。

step3 M-step：

根据E-step计算出的隐变量后验概率分布，进一步计算新的\(\theta^{(t+1)}\)

\(\alpha_k^{(t+1)} = \frac{1}{N}\sum_{i=1}^n\gamma_t(z^{(i)}_k)\)

\(\mu_k^{(t+1)} = \frac{\sum_{i=1}^n[\gamma_t(z^{(i)}_k)x_i]}{\sum_{i=1}^n\gamma_t(z^{(i)}_k)}\)

\(\Sigma_k^{(t+1)} = \frac{\sum_{i=1}^n\gamma_t(z^{(i)}_k)(x_n-\mu_k)(x_n-\mu_k)^T}{\sum_{i=1}^n\gamma_t(z^{(i)}_k)}\)

step4:

循环E-step和M-step直至收敛。

代码实现

前置说明

由于多维高斯分布概率密度函数对于个人而言不太好实现（其实是因为没学，可能后面会开一篇文章讲多维高斯分布概率密度函数的计算），所以这里就以服从一维高斯分布的数据作为手动代码实现的训练集。即训练集只有一个特征。

数据生成

这里使用sklearn的make_blobs函数生成数据。

make_blobs聚类数据生成器

scikit中的make_blobs方法常被用来生成聚类算法的测试数据，make_blobs会根据用户指定的特征数量、中心点数量、范围等来生成几类数据。

其中：

  • n_samples是待生成的样本的总数
  • n_features是每个样本的特征数
  • centers表示聚类中心点个数，可以理解为种类数。当centers为列表时，为每个类别指定中心位置。
  • cluster_std设置每个类别的方差
  • random_state是随机种子

下面将通过两个例子来直观说明make_blobs函数。

绘制数据时会用到plt.hist函数，详见python--plt.hist函数的输入参数和返回值的解释。

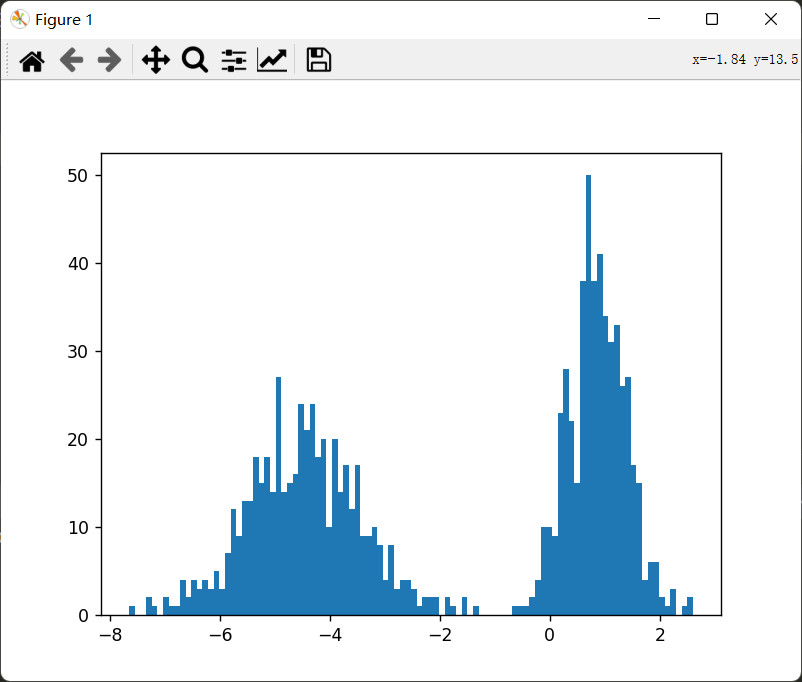
  1. 生成1000个数据：特征只有一列，分为两簇，两簇的方差为0.5和1：
1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
from sklearn.datasets._samples_generator import make_blobs

# 生成样本集

centers = 2
X,y = make_blobs(n_samples=1000,n_features=1,centers=centers,cluster_std=[0.5,1],random_state=100)
plt.hist(X,bins = 100)
plt.show()
image-20221003133732791
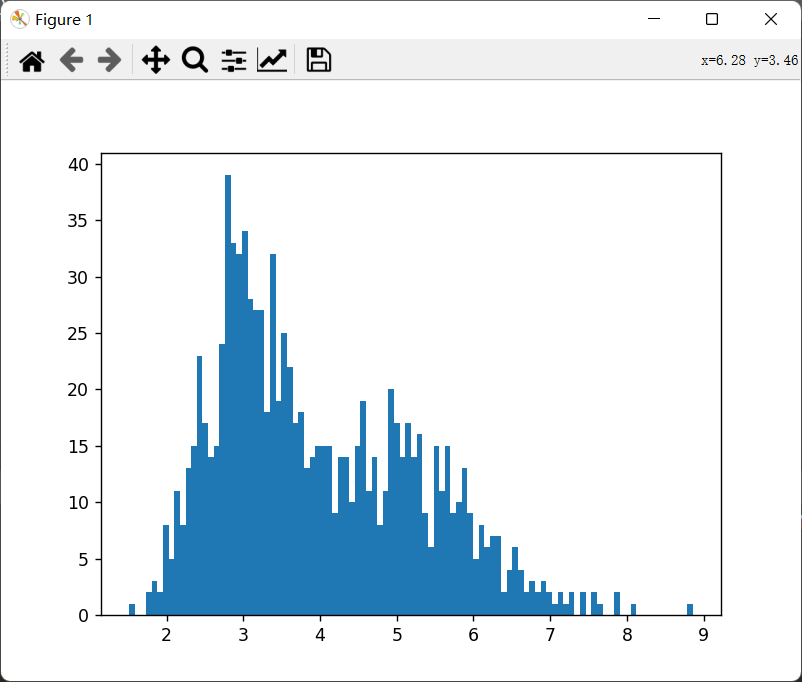
  1. 生成1000个数据：特征只有一列，分为两簇，两簇中心点为2和5，方差为0.5和1：
1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
from sklearn.datasets._samples_generator import make_blobs

# 生成样本集
centers = [[3],[5]]
X,y = make_blobs(n_samples=1000,n_features=1,centers=centers,cluster_std=[0.5,1],random_state=100)
plt.hist(X,bins = 100)
plt.show()

image-20221003142413580

可以看到上图为两个一维高斯分布混在了一起。接下来将使用上图所示数据集作为我们手动实现GMM的训练集。

GMM算法手动实现（仅对于一维高斯分布）

E-step

对于一维高斯分布概率密度函数，求解： \[ \gamma_t(z_k^{(i)}) = \frac{\alpha_k^{(t)}N(x|\mu_k^{(t)},\Sigma_k^{(t)})}{\sum_{j=1}^K \alpha_j^{(t)}N(x|\mu_j^{(t)},\Sigma_j^{(t)})} \] 其中， \[ N(x|\mu,\Sigma) = \frac {1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \] 本来打算把一维高斯分布概率密度函数写成代码的形式，但是途中发现了scipy科学计算包，这里就顺带理一下scipy中的高斯分布使用方法：【Python笔记】Scipy.stats.norm函数解析。相关参数解释都在这篇文章里了，建议先看文章。当然如果觉得太麻烦了，就直接自己把上面的概率密度函数变成代码形式就好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def E_step(data,theta):
    Rz = []
    # 计算分子
    Rz1_up = theta['w1']*stats.norm(theta['mu1'],theta['sigma1']).pdf(data)
    Rz2_up = theta['w2']*stats.norm(theta['mu2'],theta['sigma2']).pdf(data)
    # 分母
    Rz_down = theta['w1']*stats.norm(theta['mu1'],theta['sigma1']).pdf(data)+theta['w2']*stats.norm(theta['mu2'],theta['sigma2']).pdf(data)
    # 第K个隐变量的后验概率
    Rz1 = Rz1_up/Rz_down
    Rz2 = Rz2_up/Rz_down
    Rz.append(Rz1)
    Rz.append(Rz2)
    Rz = np.array(Rz)
    return Rz

M-step

计算：

\(\alpha_k^{(t+1)} = \frac{1}{N}\sum_{i=1}^n\gamma_t(z^{(i)}_k)\)

\(\mu_k^{(t+1)} = \frac{\sum_{i=1}^n[\gamma_t(z^{(i)}_k)x_i]}{\sum_{i=1}^n\gamma_t(z^{(i)}_k)}\)

\(\Sigma_k^{(t+1)} = \frac{\sum_{i=1}^n\gamma_t(z^{(i)}_k)(x_n-\mu_k)(x_n-\mu_k)^T}{\sum_{i=1}^n\gamma_t(z^{(i)}_k)}\)

前两个没什么好说明的，最后一个需要注意：因为示例是一维的，所以\(x_n-\mu_k\) 是数字，倒置也是他自己，所以分子后面那一块变成了求平方。另外，\(\Sigma\) 是\(\sigma^2\) ,求出来后需要开平方才是我们需要的\(\sigma\)。

1
2
3
4
5
6
7
8
def M_step(data,theta,Rz,n):
    theta['w1'] = np.sum(Rz[0])/n
    theta['w2'] = np.sum(Rz[1])/n
    theta['mu1'] = np.sum(Rz[0]*data)/np.sum(Rz[0])
    theta['mu2'] = np.sum(Rz[1]*data)/np.sum(Rz[1])
    Sigma1 = np.sum(Rz[0]*np.square(data-theta['mu1']))/(np.sum(Rz[0]))
    Sigma2 = np.sum(Rz[1]*np.square(data-theta['mu2']))/(np.sum(Rz[1]))
    theta['sigma1'],theta['sigma2'] = np.sqrt(Sigma1),np.sqrt(Sigma2)

初始化未知参数以及迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def run_GMM(data,times):
    # 初始化
    theta = {}
    theta['w1'],theta['w2'] = 0.5,0.5
    theta['mu1'],theta['mu2'] = 0,10
    theta['sigma1'],theta['sigma2'] = 0.8,0.8
    n = len(data)
    data = np.array(data)

    for t in range(times):
        Rz = E_step(data,theta)
        M_step(data,theta,Rz,n)
        if t % 100 == 0:
            print(theta)
            print("=========")

然后我们可以运行看看效果：

1
2
3
4
5
6
7
if __name__ == '__main__':
    # 生成样本集
    centers = [[3], [5]]
    X_train, y_test = make_blobs(n_samples=1000, n_features=1, centers=centers, cluster_std=[0.5, 1], random_state=100)
    # plt.hist(X, bins=100)
    # plt.show()
    run_GMM(data=X_train,times=1000)

可以看到，最后GMM收敛到了下面所示的值：

1
2
{'w1': 0.467708978482864, 'w2': 0.5322910215171359, 'mu1': 2.9671070095836107, 'mu2': 4.878609055231818, 'sigma1': 0.4970731536722904, 'sigma2': 1.0992431014967026}
=========

对比我们生成数据时的各个参数，发现mu和sigma差别都不大。它成功的从高斯混合模型中分离了两个高斯模型。并且与我们最初设置这两个高斯模型的参数差别不大。

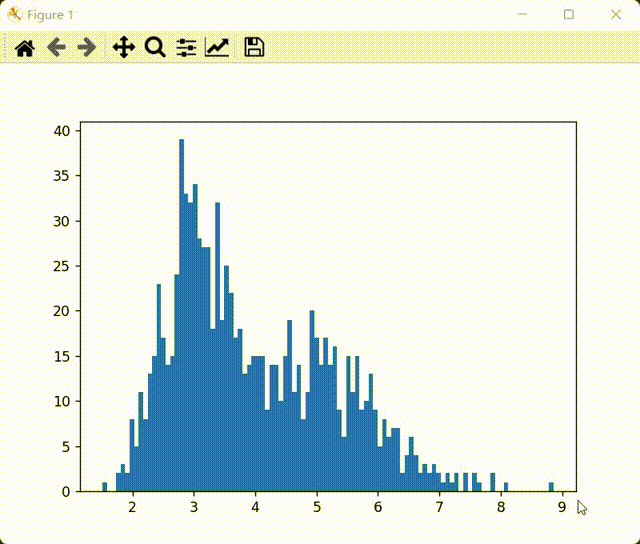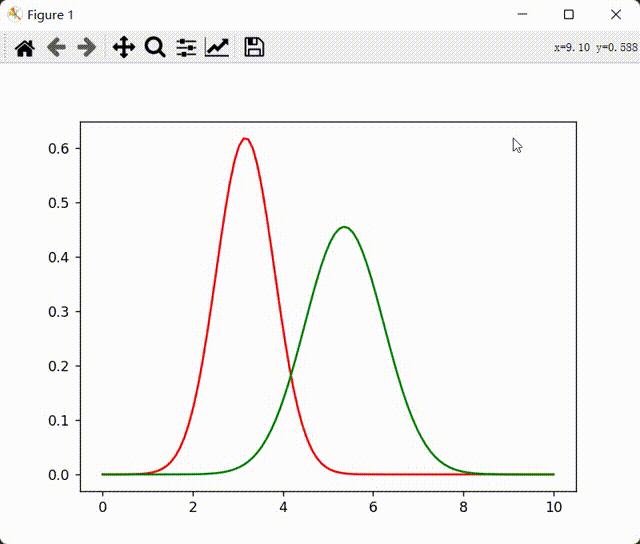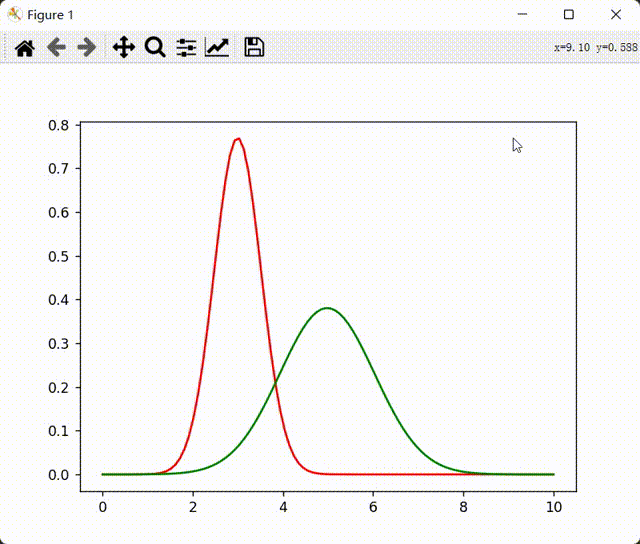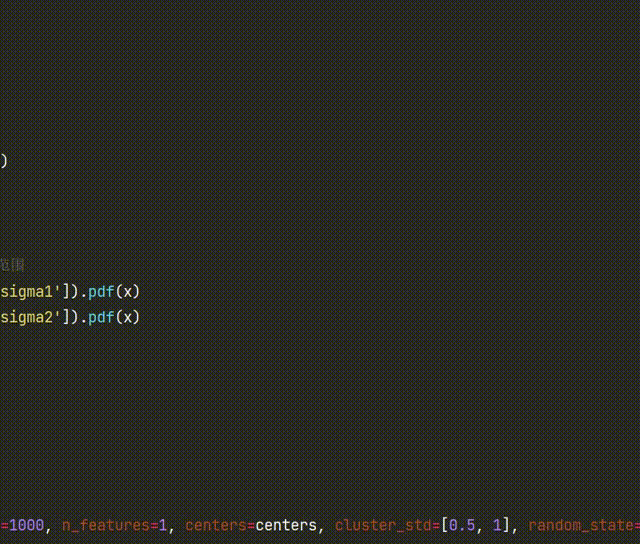
绘制可视化动态图像

这部分是可选内容，觉得比较好玩的可以试试。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def draw_GMM(thetas):
    x = np.linspace(0, 10, 100)  # 设置画图范围
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    # ax.hist(X_train, bins=100)
    plt.ion()
    for theta in thetas:
        y_1 = stats.norm(theta['mu1'], theta['sigma1']).pdf(x)
        y_2 = stats.norm(theta['mu2'], theta['sigma2']).pdf(x)
        lines1 = ax.plot(x, y_1,c='red')
        lines2 = ax.plot(x, y_2,c='green')
        plt.pause(0.3)
        try:
            ax.lines.remove(lines1[0])
            ax.lines.remove(lines2[0])
        except Exception:
            pass

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets._samples_generator import make_blobs
from scipy import stats

def draw_GMM(thetas):
    x = np.linspace(0, 10, 100)  # 设置画图范围
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    # ax.hist(X_train, bins=100)
    plt.ion()
    for theta in thetas:
        y_1 = stats.norm(theta['mu1'], theta['sigma1']).pdf(x)
        y_2 = stats.norm(theta['mu2'], theta['sigma2']).pdf(x)
        lines1 = ax.plot(x, y_1,c='red')
        lines2 = ax.plot(x, y_2,c='green')
        plt.pause(0.3)
        try:
            ax.lines.remove(lines1[0])
            ax.lines.remove(lines2[0])
        except Exception:
            pass

def E_step(data,theta):
    Rz = []
    # 计算分子
    Rz1_up = theta['w1']*stats.norm(theta['mu1'],theta['sigma1']).pdf(data)
    Rz2_up = theta['w2']*stats.norm(theta['mu2'],theta['sigma2']).pdf(data)
    # 分母
    Rz_down = theta['w1']*stats.norm(theta['mu1'],theta['sigma1']).pdf(data)+theta['w2']*stats.norm(theta['mu2'],theta['sigma2']).pdf(data)
    # 第K个隐变量的后验概率
    Rz1 = Rz1_up/Rz_down
    Rz2 = Rz2_up/Rz_down
    Rz.append(Rz1)
    Rz.append(Rz2)
    Rz = np.array(Rz)
    return Rz

def M_step(data,theta,Rz,n):
    theta['w1'] = np.sum(Rz[0])/n
    theta['w2'] = np.sum(Rz[1])/n
    theta['mu1'] = np.sum(Rz[0]*data)/np.sum(Rz[0])
    theta['mu2'] = np.sum(Rz[1]*data)/np.sum(Rz[1])
    Sigma1 = np.sum(Rz[0]*np.square(data-theta['mu1']))/(np.sum(Rz[0]))
    Sigma2 = np.sum(Rz[1]*np.square(data-theta['mu2']))/(np.sum(Rz[1]))
    theta['sigma1'],theta['sigma2'] = np.sqrt(Sigma1),np.sqrt(Sigma2)


def run_GMM(data,times):
    # 初始化
    theta = {}
    draw_theta = []
    theta['w1'],theta['w2'] = 0.5,0.5
    theta['mu1'],theta['mu2'] = 0,10
    theta['sigma1'],theta['sigma2'] = 0.8,0.8
    n = len(data)
    data = np.array(data)

    for t in range(times):
        Rz = E_step(data,theta)
        M_step(data,theta,Rz,n)
        if t<=50:
            print(theta)
            print("=========")
            draw_theta.append(theta.copy())
    draw_GMM(draw_theta)

if __name__ == '__main__':
    # 生成样本集
    centers = [[3], [5]]
    X_train, y_test = make_blobs(n_samples=1000, n_features=1, centers=centers, cluster_std=[0.5, 1], random_state=100)
    plt.hist(X_train,100)
    plt.show()
    run_GMM(data=X_train,times=650)

可视化演示

原始数据：

image-20221003142413580

训练结果：

1664799029453

使用sklearn的GMM

又到了令人愉悦的部分了。

这部分将使用sklearn的GMM来实现聚类，为了便于画图，这里特征只选两个。即二维高斯混合模型。另外顺带一提，如果你稍微查看了sklearn中GMM的源码，就会发现它在初始化时就是先用了一次Kmean。

关于sklearn的GMM用法就不多说了，推荐一篇文章：Scikit-Learn学习笔记——高斯混合模型(GMM)应用：分类、密度估计、生成模型_盐味橙汁的博客-CSDN博客_高斯混合模型分类

这篇文章还说明了GMM在密度估计、生成模型上的应用。

代码

注：绘制边缘椭圆部分搬的是这篇文章的代码，因为本人还不太会。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.mixture import GaussianMixture
from sklearn.datasets._samples_generator import make_blobs

def creat_data(centers,size = 1000):
    X,labels = make_blobs(n_samples=size,n_features=2,centers=centers,cluster_std=1,random_state=100)
    # 把X训练集变为椭圆的形式
    rng = np.random.RandomState(12)
    X = np.dot(X, rng.randn(2, 2))
    return X,labels

def draw_ellipse(position, covariance, ax=None, **kwargs):
    """用给定的位置和协方差画一个椭圆"""
    ax = ax or plt.gca()

    #将协方差转换为主轴
    if covariance.shape == (2, 2):
        U, s, Vt = np.linalg.svd(covariance)
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
        width, height = 2 * np.sqrt(s)
    else:
        angle = 0
        width, height = 2 * np.sqrt(covariance)

    #画出椭圆
    for nsig in range(1, 4):
        ax.add_patch(Ellipse(position, nsig * width, nsig * height, angle, **kwargs))

def plot_gmm(gmm, X,labels, label=True, ax=None):
    ax = ax or plt.gca()
    if label:
        ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
    else:
        ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
    w_factor = 0.2 / gmm.weights_.max()
    for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
        draw_ellipse(pos, covar, alpha=w * w_factor)
    plt.show()

if __name__ == '__main__':
    centers = 5
    X,labels = creat_data(centers = centers)
    # 创建并训练高斯混合模型
    model = GaussianMixture(n_components = centers,covariance_type='full')
    model.fit(X)
    # 预测
    labels_predict = model.predict(X)
    # 绘制图像
    plot_gmm(model, X,labels_predict)

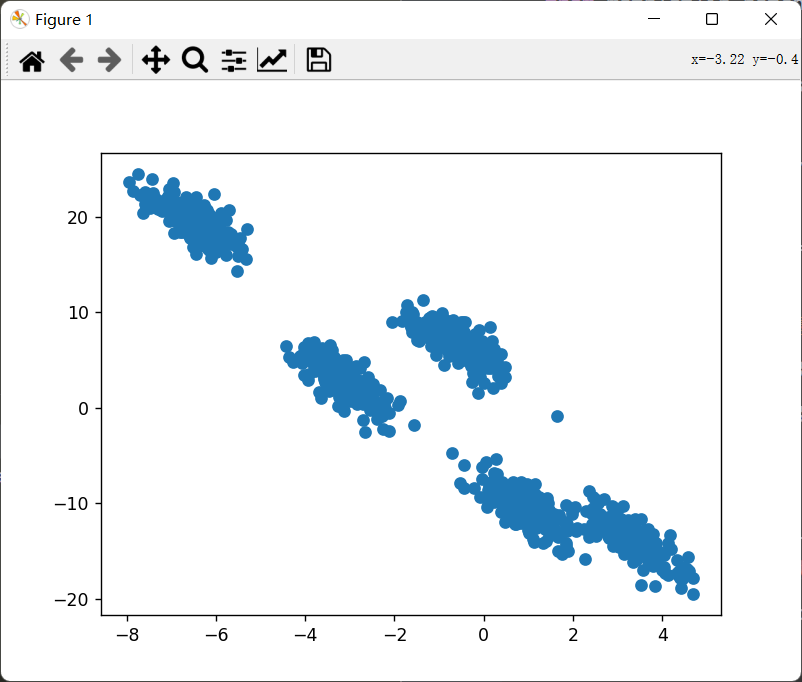
原始数据：

image-20221004202410089

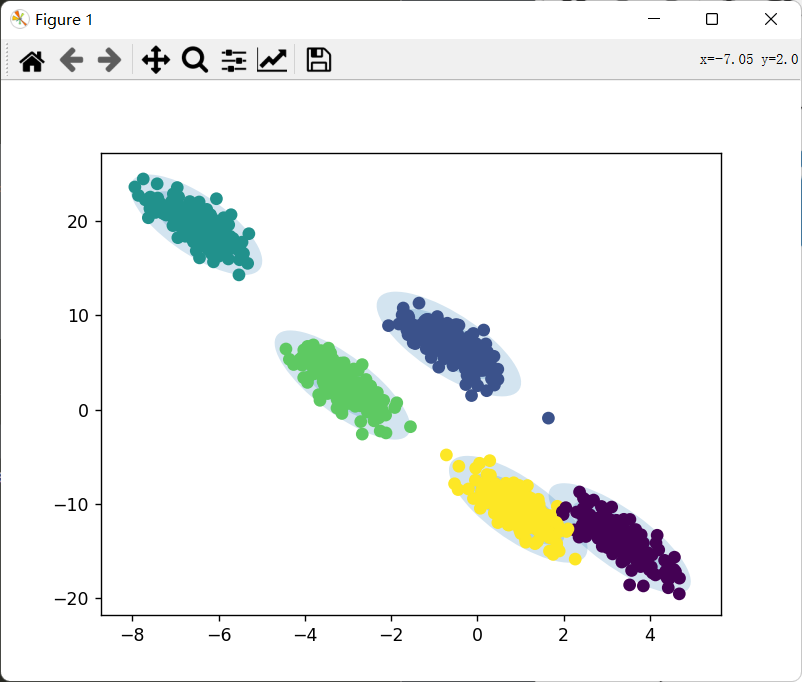
经过聚类后的数据：

image-20221004202456739