前言

在阅读本文之前，请确保已经对Softmax多分类器的原理、相关公式推导、具体流程有一定了解。本文将不再具体介绍这些内容，若对这些内容还不了解，请先阅读本文的前置文章。

本文为softmax多分类器下篇，共分为两个部分：

第一部分：对softmax分类器具体代码实现，并将鸢尾花数据集作为示例，进行模型训练和预测。

第二部分：使用sklrean实现softmax分类器，并与自己实现的softmax分类器作结果对比。（但好像sklrean只有逻辑回归的包，但是达到了多分类的效果，所以一般说sklrean里的softmax就是逻辑回归）

关于代码

关于本文代码实现的一些说明：

本篇文章涉及的部分已经在本系列以前的文章中具体介绍并实现过模块例如：训练集测试集拆分、Z-score标准化、测试结果评估等将不再手动实现。

另外，因为没有找到合适的参考文章，所以这是一次在没有任何参考，仅通过个人理解和公式推导的前提下实现的代码。如果有不足的地方还请指出。

第一部分

在该部分，将会对softmax分类器进行具体实现，并完成鸢尾花多分类示例。

Softmax分类器相关公式与步骤

回顾上篇文章我们总结的softmax相关公式与步骤。

梯度下降步骤

给定训练集X，训练集X共分为K类:

随机初始化模型未知参数\(\theta\) ，本篇文章中为随机初始化权重向量\(w_k,b_k,k=1,2,...,K-1\)。其中，\(w_k\)为向量，\(b_k\) 为标量。
梯度下降算法迭代更新模型参数直至收敛，每一轮具体流程如下：
1. 先通过正向传播求得本轮训练样本预测值。
2. 反向传播更新模型参数：
\[ \begin{split} & w_k = w_k - a\frac{\partial J}{\partial w_k} = w_k-a\frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k)x,\quad k = 0,1,...,K-1 \\ & b_k = b_k -a\frac{\partial J}{\partial b_k} = b_k-a\frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k),\quad k = 0,1,...,K-1 \end{split} \]
注意：上述公式省去了上标i，上标i表示这是第i个样本。

数据集获取

鸢尾花数据集的两种获取方式:

sklrean自带鸢尾花数据集，不需要额外下载。
鸢尾花数据集下载地址：Iris Species | Kaggle

我专门查看了两个数据集，没有区别。

从零开始实现softmax多分类器

为了使代码更便于调用，层次更加清晰，本次将会以面向对象的形式实现模型。（之前好几次都是直接写的函数）如果觉得分开写的太乱，可以看最后给出的组合起来的完整代码。

导入数据

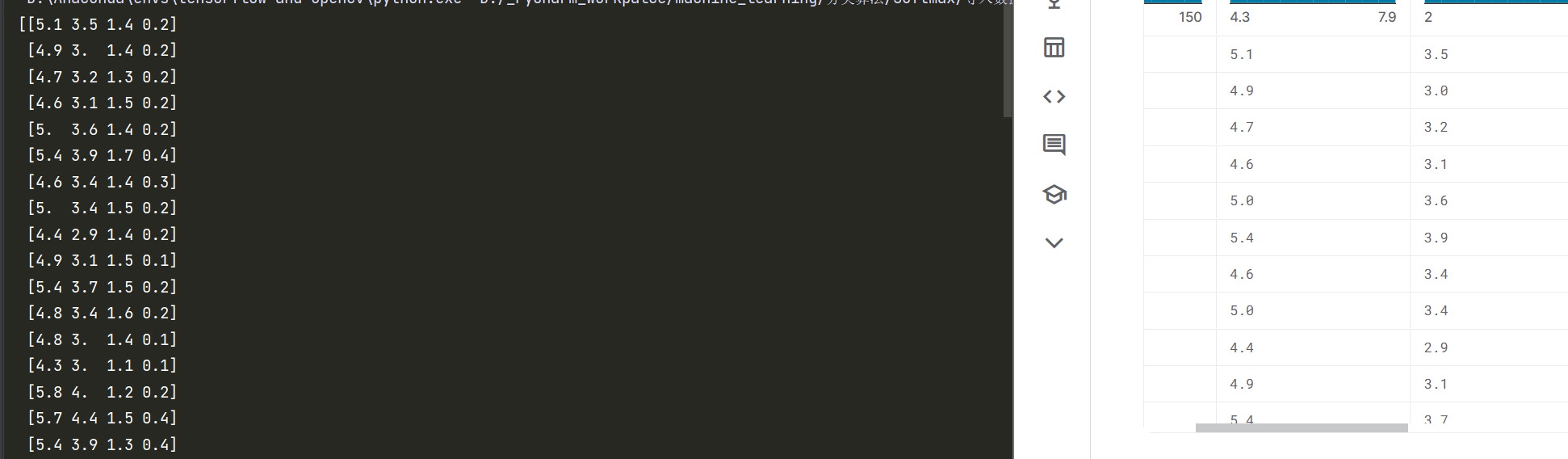
为了便于编写代码过程中对各模块作测试，这里先导入鸢尾花数据集，我采用第一种导入数据集的方法。

import numpy as np
from sklearn import datasets

if __name__ == '__main__':
    iris = datasets.load_iris() # 导入鸢尾花数据集
    dataSet = iris.data # 特征集
    target = iris.target # label集

初始框架

先把softmax类的框架搭出来，之后的函数一个个加进来。

class SoftmaxModel:

    def __init__(self,random_state = None):
        """
        初始化模型
        :param random_state: 指定随机种子，默认为None
        """
        self.__random_state = random_state
        self.__theta = None # 模型参数

step1:将label向量化

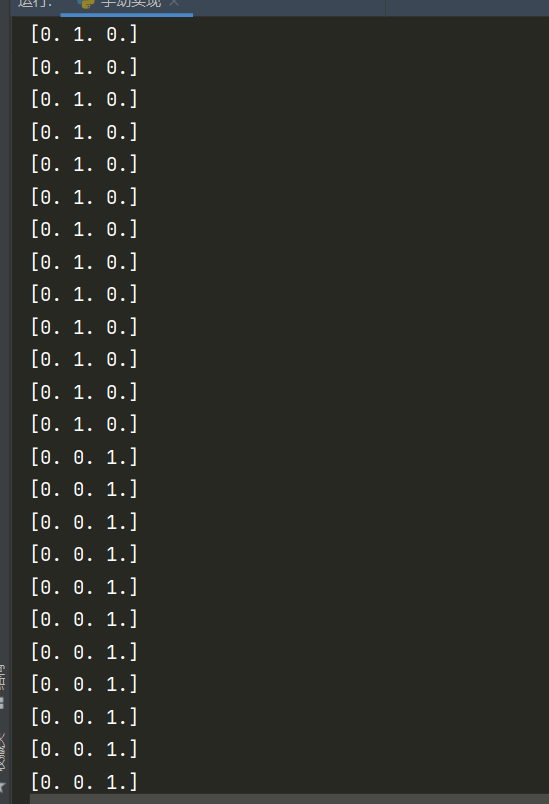
根据上一篇的推导，我们在进行softmax分类时，需要先将\(y = c_k\)的形式换成\((0,..,1,...,0)\)的形式。

def __labelTransform(self,Y,classes):
    """
    将label向量化
    :param Y: label集合
    :param classes: 共有多少类
    :return: 向量化后的label集
    """
    vec_Y = []
    for y in Y:
        vec_label = np.zeros(classes)
        vec_label[y] = 1
        vec_Y.append(vec_label)
    return vec_Y

测试：

只截取了部分。可以看到label成功变成了我们需要的。

step2:根据训练集初始化模型参数

这部分需要写的比较杂，不好单独抽成函数，所以大部分细节就在代码说。另外，如有疑问的地方，请配合上一篇文章一起阅读。

初始化W：维度为（K，M）。一共有K个\(w_k\)(K为类别数)，每一个\(w_k\)都是向量，维度与单个样本\(x\)相同。
初始化时B一共有K个，每一个\(b_k\)都是标量。

import numpy as np
from sklearn import datasets

class SoftmaxModel:

    def __init__(self,random_state = None):
        """
        初始化模型
        :param random_state: 指定随机种子，默认为None
        """
        self.__random_state = random_state
        self.__theta = None # 模型参数

    def __labelTransform(self,Y,classes):
        """
        将label向量化
        :param Y: label集合
        :param classes: 共有多少类
        :return: 向量化后的label集
        """
        vec_Y = []
        for y in Y:
            vec_label = list(np.zeros(classes))
            vec_label[y] = 1
            vec_Y.append(vec_label)
        vec_Y = np.array(vec_Y)
        return vec_Y

    def __init_theta(self,classes,feature_nums,random_state):
        """
        初始化模型参数
        :param classes: 一共有多少类，即K
        :param feature_nums: 样本特征数目
        :param random_state: 随机种子
        :return: 模型参数
        """
        theta = {}
        np.random.seed(random_state)
        theta['W'] = np.random.randn(classes,feature_nums) # 关于randn的用法请自行查找
        theta['B'] = np.random.randn(classes)
        return theta



    def train(self,X,Y,classes = None,learning_rate = 1e-3,num_iters = 100):
        """
        训练softmax模型，此时采用的批量梯度下降算法。
        :param X: 样本集
        :param Y: 标签集，请确保类别标号从0开始
        :param classes: 共有多少个类别，如果为None，则会根据Y自动调整
        :param learning_rate: 学习率，默认0.001
        :param num_iters: 最大迭代次数，默认100次
        :return:
        """

        # 设置模型类别数
        if classes == None:
            self.__classes = np.max(Y) + 1
        else:
            self.__classes = classes
        # 将label向量化
        Y = self.__labelTransform(Y,self.__classes)
        # 根据样本调整W的维度，并进行初始化
        sample_nums,feature_nums = X.shape # 行为样本个数，列为特征数
        # 初始化参数
        if self.__theta is None:
            self.__theta = self.__init_theta(self.__classes,feature_nums,self.__random_state)
        for k in range(self.__classes):
            print(f"w_{k} is {self.__theta['W'][k]},b_{k} is {self.__theta['B'][k]}")

if __name__ == '__main__':
    iris = datasets.load_iris() # 导入鸢尾花数据集
    dataSet = iris.data # 特征集
    target = iris.target # label集
    # print(dataSet)
    model = SoftmaxModel(random_state=10)
    model.train(dataSet,target,learning_rate = 1e-3,num_iters = 100)

输出：

step3:对特征进行加权组合

公式： \[ z_k = w_k^Tx+b_k = (\sum_{i=1}^Mw_{k,i}x_i)+b_k \] 函数变量说明：

X：样本集，维度为(N，M)，代表N个样本，每个样本M个特征。
W：权值，维度为（K，M）。
B：维度为（1，K）。
Z：维度为（N，K），第i行代表由第i个样本线性组合输出的\(z\)。

矩阵乘法： \[ A(N,M)\cdot B(M,K) = C(N,K) \] 所以\(X\cdot W^T\)即可得没有加B的Z。

矩阵加法，两个尺寸一样的才可以加。所以需要把B按行复制N次，得到B（N，K），然后与Z相加即可。

def __linear_combination(self,X,theta):
    """
    对样本特征进行线性加权组合
    :param X: 特征集
    :param theta: 模型参数
    :return: Z,加权后的输出
    """
    Z = np.dot(X,theta['W'].T)+np.tile(theta['B'],(X.shape[0],1))
    return Z

step4:softmax激活函数

下一步应该是对Z进行softmax激活，得到每一个后验概率\(P(y=c_k|x,\theta)\)。（后验概率就是所谓的预测概率）

公式： \[ softmax(z_k) = a_k = \frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}},~~~~k = 0,1,...,K-1 \] 函数变量说明：

A：维度（N，K），第i行代表第i个样本对应的后验概率分布\(a^i\),第k列对应该样本对第k类的后验概率\(a_k\)。
Z：维度（N，K），上一步已经说过Z的含义。

要想从Z求到A,根据公式，要先对整个矩阵Z求\(expZ = exp(Z)\),然后分母为expZ按行求和，分子为expZ[i,k]。

def __cal_softmax(self,Z):
    """
    通过softmax激活，计算后验概率
    :param Z: 隐藏层输出
    :return: A,后验概率矩阵
    """
    expZ = np.exp(Z)
    A = np.zeros_like(expZ)
    denominator = np.sum(expZ,axis=1) # 计算分母
    N = expZ.shape[0]
    for i in range(N):
        A[i] = expZ[i]/denominator[i]
    return A

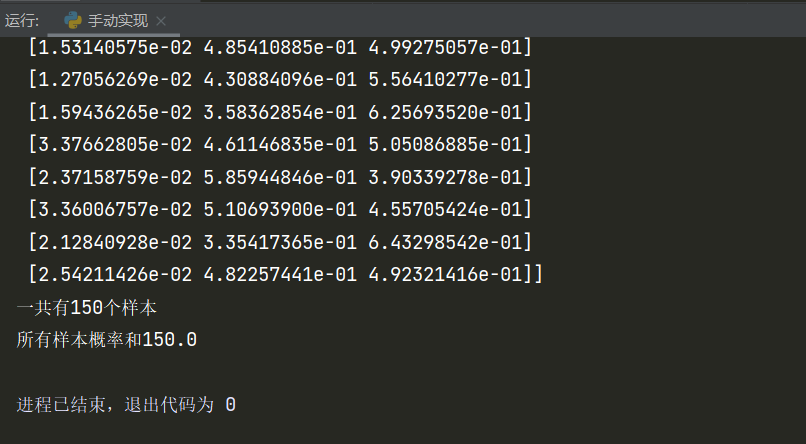
我们可以检测一下后验概率计算的对不对，因为一个样本对应的后验分布之和为1，那么有多少样本，所有后验概率之和就应该是多少：

聪明的小伙伴已经想到了，到这一步就完成了正向传播。现在只需要知道模型参数，我们就可以对某个未知分类的样本作预测。

step5:计算交叉熵损失函数

其实这一步在训练时用不到，不过既然有公式还是实现了吧，然后来对刚才我们计算的后验概率求一个代价函数。

注：代价函数为损失函数求平均。

公式： \[ \begin{split} & L(\hat y,y) = -\sum_{k=1}^Ky_kloga_k \\ & J = \frac{1}{N}\sum_{i=0}^{N-1}L(\hat y,y) = -\frac{1}{N}\sum_{i=0}^{N-1}\sum_{k=1}^Ky_kloga_k \end{split} \] 函数变量说明：

A和Y都是维度为（N，K）的矩阵，也就是说只需要一一对应求出\(-y^i_kloga^i_k\) ,然后对整个矩阵求和，然后取相反数，最后除N就行了。

一般log都是以2为底。

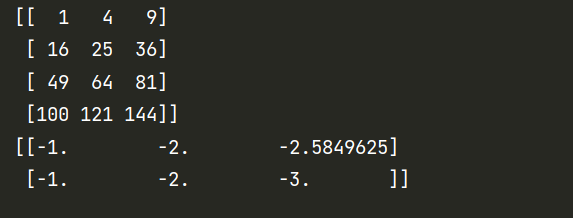
现在先测试一下我们需要的函数：

A = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
B = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
C = -np.log2(np.array([[2,4,6],[2,4,8]]))
print(np.multiply(A,B))
print(C)

ok,没问题。现在实现该部分的代码：

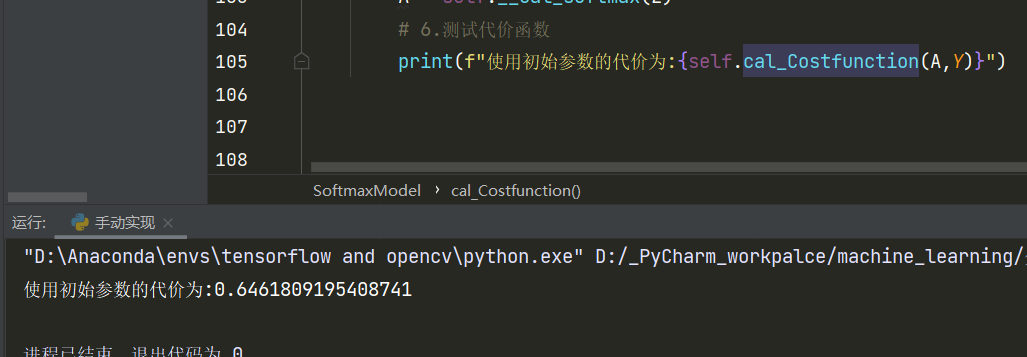
def cal_Costfunction(self,A,Y):
    """
    计算代价函数
    :param A: 后验概率矩阵（预测概率矩阵）
    :param Y: 真实label矩阵
    :return: 代价
    """
    J = -np.sum(np.multiply(Y,np.log2(A)))
    J /= Y.shape[0]
    return J

step6：单轮模型参数迭代

每一轮参数迭代公式： \[ \begin{split} & w_k = w_k - a\frac{\partial J}{\partial w_k} = w_k-a\frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k)x,\quad k = 0,1,...,K-1 \\ & b_k = b_k -a\frac{\partial J}{\partial b_k} = b_k-a\frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k),\quad k = 0,1,...,K-1 \end{split} \] 函数变量说明：

\(\alpha\)：超参数，这个就不多说了，我们需要手动调整。
A：维度（N，K），含义与之前一样，后验概率矩阵。
Y：维度（N，K），含义与之前一样，真实label矩阵。
X：维度（N，M）。N个样本，一个样本M个特征。
W：维度（K，M），权值矩阵。K对应\(z_k\)，M对应\(x\)的特征。
B：维度（1，K），标量。K对应\(z_k\)。

这一步想矩阵化运算有点绕，所以我得分三步说明：

1.只看单个样本\(x\): \[ w_k = w_k-\alpha(a_k-y_k)x \]

\(w_k\)：维度（1，M）
\(a_k-y_k\)：标量
\(x\):维度（1,M）

所以只看一个样本时，为\(a_k-y_k\) （标量）去乘x里每一个特征，然后再乘学习率。

2.拓展到N个样本X的平均\(w_k\)： \[ w_k = w_k-\alpha\frac{1}{N}(A_k-Y_k)^TX \] 现在\(A_k-Y_k\)维度应该是\((N,1)\)。也就是每个类别对应的那一列的预测值与真实值相减。然后将其倒置变成\((1,N)\)去乘\(X(N,M)\),就可以得到\((1,M)\)维度,不过这时求得的是所有样本对应的\(w_k\)之和，所以还要对\((1,M)\)除个N，才是\(w_k\)的均值。

3.拓展到W \[ W = W-a\frac{1}{N}(A-Y)^TX \] 在草稿本上自己算一下，应该可以想明白为什么求和符号消失了。

同理， \[ B = B-a\frac{1}{N}\sum_{axis=0}(A-Y) \] \(axis=0\) 代表对列求和。

def __gradient_iteration(self,W,B,X,Y,A,learning_rate):
    """
    一轮梯度迭代
    :param W: W
    :param B: B
    :param X: X
    :param Y: Y
    :param A: A
    :param learning_rate: 学习率
    :return: 更新后的W,B
    """
    A_Y = A-Y
    W = W-(learning_rate/X.shape[0])*np.dot(A_Y.T,X)
    B = B-(learning_rate/X.shape[0])*np.sum(A_Y,axis=0)
    return W,B

step7：梯度下降，整合模型训练模块代码

线性代数给我推麻了，哎。不过最后好歹还是推出来了。

截止目前，训练过程的代码已经可以进行整合了，我们来测试一下效果：

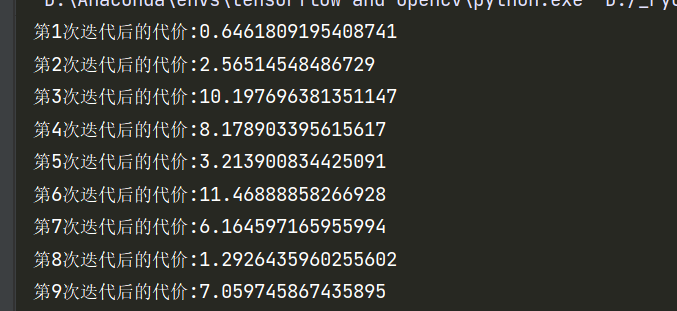
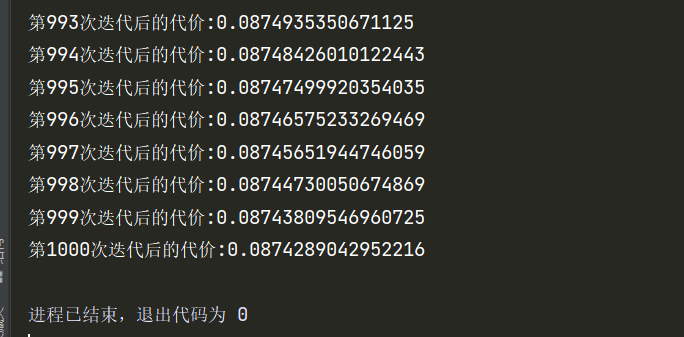
import numpy as np
from sklearn import datasets

class SoftmaxModel:

    def __init__(self,random_state = None):
        """
        初始化模型
        :param random_state: 指定随机种子，默认为None
        """
        self.__random_state = random_state
        self.__theta = None # 模型参数

    def __labelTransform(self,Y,classes):
        """
        将label向量化
        :param Y: label集合
        :param classes: 共有多少类
        :return: 向量化后的label集
        """
        vec_Y = []
        for y in Y:
            vec_label = list(np.zeros(classes))
            vec_label[y] = 1
            vec_Y.append(vec_label)
        vec_Y = np.array(vec_Y)
        return vec_Y

    def __init_theta(self,classes,feature_nums,random_state):
        """
        初始化模型参数
        :param classes: 一共有多少类，即K
        :param feature_nums: 样本特征数目
        :param random_state: 随机种子
        :return: 模型参数
        """
        theta = {}
        np.random.seed(random_state)
        theta['W'] = np.random.randn(classes,feature_nums) # 关于randn的用法请自行查找
        theta['B'] = np.random.randn(classes)
        return theta

    def __linear_combination(self,X,theta):
        """
        对样本特征进行线性加权组合
        :param X: 特征集
        :param theta: 模型参数
        :return: Z,加权后的输出
        """
        Z = np.dot(X,theta['W'].T)+np.tile(theta['B'],(X.shape[0],1))
        return Z

    def __cal_softmax(self,Z):
        """
        通过softmax激活，计算后验概率
        :param Z: 隐藏层输出
        :return: A,后验概率矩阵
        """
        expZ = np.exp(Z)
        A = np.zeros_like(expZ)
        denominator = np.sum(expZ,axis=1) # 计算分母
        N = expZ.shape[0]
        for i in range(N):
            A[i] = expZ[i]/denominator[i]
        return A

    def cal_Costfunction(self,A,Y):
        """
        计算代价函数
        :param A: 后验概率矩阵（预测概率矩阵）
        :param Y: 真实label矩阵
        :return: 代价
        """
        J = -np.sum(np.multiply(Y,np.log2(A)))
        J /= Y.shape[0]
        return J

    def __gradient_iteration(self,W,B,X,Y,A,learning_rate):
        """
        一轮梯度迭代
        :param W: W
        :param B: B
        :param X: X
        :param Y: Y
        :param A: A
        :param learning_rate: 学习率
        :return: 更新后的W,B
        """
        A_Y = A-Y
        W = W-(learning_rate/X.shape[0])*np.dot(A_Y.T,X)
        B = B-(learning_rate/X.shape[0])*np.sum(A_Y,axis=0)
        return W,B

    def train(self,X,Y,classes = None,learning_rate = 0.001,num_iters = 100):
        """
        训练softmax模型，此时采用的批量梯度下降算法。
        :param X: 样本集
        :param Y: 标签集，请确保类别标号从0开始
        :param classes: 共有多少个类别，如果为None，则会根据Y自动调整
        :param learning_rate: 学习率，默认0.001
        :param num_iters: 最大迭代次数，默认100次
        :return:
        """

        # 1.设置模型类别数
        if classes == None:
            self.__classes = np.max(Y) + 1
        else:
            self.__classes = classes
        # 2.将label向量化
        Y = self.__labelTransform(Y,self.__classes)
        # 3.根据样本调整W的维度，并进行初始化
        sample_nums,feature_nums = X.shape # 行为样本个数，列为特征数
        if self.__theta is None:
            self.__theta = self.__init_theta(self.__classes,feature_nums,self.__random_state)

        # 梯度下降更新参数
        for i in range(num_iters):
            # 4.对样本特征集线性加权组合
            Z = self.__linear_combination(X, self.__theta)
            # 5.通过softmax激活函数，计算后验概率矩阵
            A = self.__cal_softmax(Z)
            self.__theta['W'],self.__theta['B'] = self.__gradient_iteration(self.__theta['W'],self.__theta['B'],X,Y,A,learning_rate)
            print(f"第{i+1}次迭代后的代价:{self.cal_Costfunction(A,Y)}")



if __name__ == '__main__':
    iris = datasets.load_iris() # 导入鸢尾花数据集
    dataSet = iris.data # 特征集
    target = iris.target # label集
    # print(dataSet)
    model = SoftmaxModel(random_state=10)
    model.train(dataSet,target,learning_rate = 0.5,num_iters = 1000)

前几次代价跳的比较厉害，这是学习率设置的原因。小了吧又下降的太慢了。这是我从很多学习率里选的一个比较合适的。看这情况后面还是收敛了。

step8：完成预测模块

这个部分就简单了，正向传播之后多加一个判断就行了：谁的概率最大选谁。

哦对，注意，预测完毕后返回的\(Y_{predict}\)应该是没有进行label向量化的状态。即如果\(y_{pre} = c_k\)，那么\(y_{pre}\)的值应该是\(k-1\)而不是一个向量。

def getTheta(self):
    """
    获取训练好的模型参数，方便下次不用重新训练
    :return: theta,模型参数
    """
    return self.__theta

def predict(self,X,theta = None):
    """
    对指定样本集进行预测
    :param X: 需要进行预测的样本
    :param theta: 方便不用每一次都训练，所以也可以直接传模型参数，默认为None
    :return: 预测结果
    """
    if theta is None:
        theta = self.__theta
    Z = self.__linear_combination(X,theta)
    A = self.__cal_softmax(Z)
    y_predict = np.argmax(A,axis=1)
    return y_predict

OK,到此最基本的softmax分类器就实现了，这是整个类的代码：

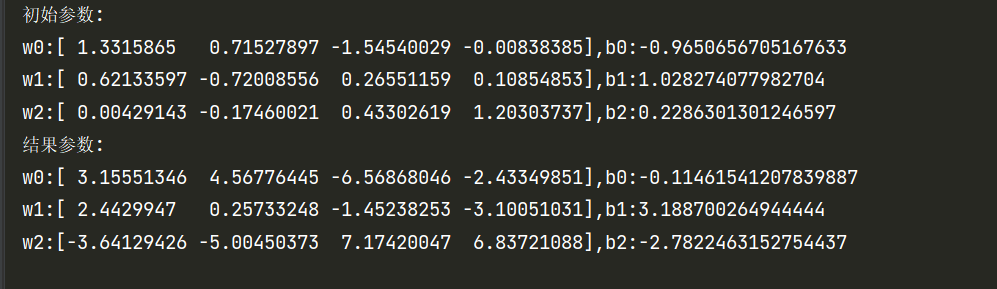
import numpy as np
class SoftmaxModel:

    def __init__(self,random_state = None):
        """
        初始化模型
        :param random_state: 指定随机种子，默认为None
        """
        self.__random_state = random_state
        self.__theta = None # 模型参数

    def __labelTransform(self,Y,classes):
        """
        将label向量化
        :param Y: label集合
        :param classes: 共有多少类
        :return: 向量化后的label集
        """
        vec_Y = []
        for y in Y:
            vec_label = list(np.zeros(classes))
            vec_label[y] = 1
            vec_Y.append(vec_label)
        vec_Y = np.array(vec_Y)
        return vec_Y

    def __init_theta(self,classes,feature_nums,random_state):
        """
        初始化模型参数
        :param classes: 一共有多少类，即K
        :param feature_nums: 样本特征数目
        :param random_state: 随机种子
        :return: 模型参数
        """
        theta = {}
        np.random.seed(random_state)
        theta['W'] = np.random.randn(classes,feature_nums) # 关于randn的用法请自行查找
        theta['B'] = np.random.randn(classes)
        return theta

    def __linear_combination(self,X,theta):
        """
        对样本特征进行线性加权组合
        :param X: 特征集
        :param theta: 模型参数
        :return: Z,加权后的输出
        """
        Z = np.dot(X,theta['W'].T)+np.tile(theta['B'],(X.shape[0],1))
        return Z

    def __cal_softmax(self,Z):
        """
        通过softmax激活，计算后验概率
        :param Z: 隐藏层输出
        :return: A,后验概率矩阵
        """
        expZ = np.exp(Z)
        A = np.zeros_like(expZ)
        denominator = np.sum(expZ,axis=1) # 计算分母
        N = expZ.shape[0]
        for i in range(N):
            A[i] = expZ[i]/denominator[i]
        return A

    def cal_Costfunction(self,A,Y):
        """
        计算代价函数
        :param A: 后验概率矩阵（预测概率矩阵）
        :param Y: 真实label矩阵
        :return: 代价
        """
        J = -np.sum(np.multiply(Y,np.log2(A)))
        J /= Y.shape[0]
        return J

    def __gradient_iteration(self,W,B,X,Y,A,learning_rate):
        """
        一轮梯度迭代
        :param W: W
        :param B: B
        :param X: X
        :param Y: Y
        :param A: A
        :param learning_rate: 学习率
        :return: 更新后的W,B
        """
        A_Y = A-Y
        W = W-(learning_rate/X.shape[0])*np.dot(A_Y.T,X)
        B = B-(learning_rate/X.shape[0])*np.sum(A_Y,axis=0)
        return W,B

    def train(self,X,Y,classes = None,learning_rate = 0.001,num_iters = 100):
        """
        训练softmax模型，此时采用的批量梯度下降算法。
        :param X: 样本集
        :param Y: 标签集，请确保类别标号从0开始
        :param classes: 共有多少个类别，如果为None，则会根据Y自动调整
        :param learning_rate: 学习率，默认0.001
        :param num_iters: 最大迭代次数，默认100次
        :return:
        """

        # 1.设置模型类别数
        if classes == None:
            self.__classes = np.max(Y) + 1
        else:
            self.__classes = classes
        # 2.将label向量化
        Y = self.__labelTransform(Y,self.__classes)
        # 3.根据样本调整W的维度，并进行初始化
        sample_nums,feature_nums = X.shape # 行为样本个数，列为特征数
        if self.__theta is None:
            self.__theta = self.__init_theta(self.__classes,feature_nums,self.__random_state)
        print("初始参数:")
        for k in range(self.__classes):
            print(f"w{k}:{self.__theta['W'][k]},b{k}:{self.__theta['B'][k]}")

        # 梯度下降更新参数
        for i in range(num_iters):
            # 4.对样本特征集线性加权组合
            Z = self.__linear_combination(X, self.__theta)
            # 5.通过softmax激活函数，计算后验概率矩阵
            A = self.__cal_softmax(Z)
            self.__theta['W'],self.__theta['B'] = self.__gradient_iteration(self.__theta['W'],self.__theta['B'],X,Y,A,learning_rate)
            # print(f"第{i+1}次迭代后的代价:{self.cal_Costfunction(A,Y)}")
        print("结果参数:")
        for k in range(self.__classes):
            print(f"w{k}:{self.__theta['W'][k]},b{k}:{self.__theta['B'][k]}")

    def getTheta(self):
        """
        获取训练好的模型参数，方便下次不用重新训练
        :return: theta,模型参数
        """
        return self.__theta

    def predict(self,X,theta = None):
        """
        对指定样本集进行预测
        :param X: 需要进行预测的样本
        :param theta: 方便不用每一次都训练，所以也可以直接传模型参数，默认为None
        :return: 预测结果
        """
        if theta is None:
            theta = self.__theta
        Z = self.__linear_combination(X,theta)
        A = self.__cal_softmax(Z)
        y_predict = np.argmax(A,axis=1)
        return y_predict

使用自己实现的softmax多分类器完成鸢尾花多分类

这部分的内容就不多解释了，还是老套路：

分割训练集和测试集（这次选择7：3）
对训练集Z-score标准化，并用训练集标准化时计算的参数去标准化测试集（可别一起丢进去标准化）
训练集丢进去训练，训练结束把测试集丢进去测试
对测试集的测试结果进行评估

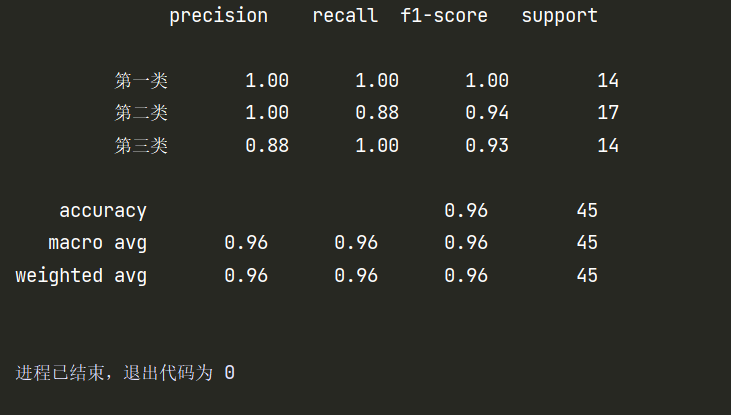
from sklearn.metrics import classification_report # 结果评估
from sklearn.model_selection import train_test_split # 拆分数据集
from sklearn.preprocessing import StandardScaler # 数据标准化
if __name__ == '__main__':
    random_state = 10
    iris = datasets.load_iris() # 导入鸢尾花数据集
    dataSet = iris.data # 特征集
    target = iris.target # label集-

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(dataSet, target, train_size=0.7, random_state=random_state)
    # 使用sklearn进行Z-score标准化
    scaler = StandardScaler()
    X_train = scaler.fit_transform(X_train)  # 标准化训练集X
    # 标准化测试集x,只有训练集才fit_transform，测试集是transform
    X_test = scaler.transform(X_test)

    # 创建模型
    model = SoftmaxModel(random_state=random_state)
    model.train(X_train,y_train,learning_rate = 0.5,num_iters = 100)
    # 预测
    y_predict =  model.predict(X_test)

    class_names = ['第一类', '第二类', '第三类']
    print(classification_report(y_test, y_predict, target_names=class_names))

评估结果：

至少通过评估结果来看，自己实现的softmax模型没什么奇怪的问题。不过可能在一些细节上还有很多改进空间。

第二部分

使用skrean中的softmax（其实是逻辑回归）

怪，我发现sklearn里没有softmax，只有逻辑回归的包，但是它那个逻辑回归的包又可以作多分类。因为原本的逻辑回归只能作二分类，所以我觉得它实现的逻辑回归可能就是softmax。因此调用的是LogisticRegression。

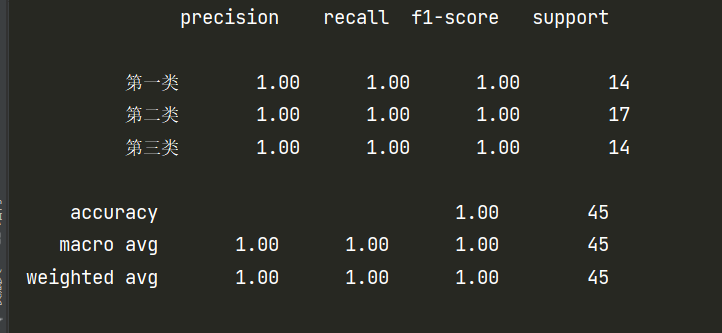
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report # 结果评估
from sklearn.preprocessing import StandardScaler # 数据标准化
from sklearn.linear_model import LogisticRegression

if __name__ == '__main__':
    random_state = 10
    iris = datasets.load_iris() # 导入鸢尾花数据集
    dataSet = iris.data # 特征集
    target = iris.target # label集

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(dataSet, target, train_size=0.7, random_state=random_state)
    # 使用sklearn进行Z-score标准化
    scaler = StandardScaler()
    X_train = scaler.fit_transform(X_train)  # 标准化训练集X
    # 标准化测试集x,只有训练集才fit_transform，测试集是transform
    X_test = scaler.transform(X_test)

    model = LogisticRegression()
    model.fit(X_train, y_train)
    y_predict = model.predict(X_test)

    class_names = ['第一类', '第二类', '第三类']
    print(classification_report(y_test, y_predict, target_names=class_names))

结果对比

看到这个结果，虽然我知道是数据集太小的原因，但我内心十分不服，于是把自己实现的分类器的迭代次数改成了1000，再跑了一次。

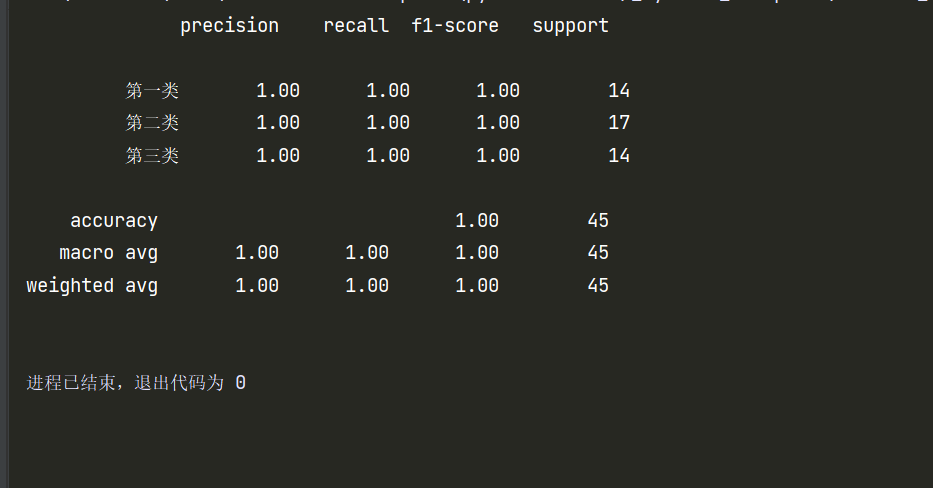
自己实现的分类器迭代次数改成迭代1000次后：

不得不说，这个数据集实在太小了，只有150个，分出来测试集才45个样本，所以预测结果才会这么好。

机器学习笔记14——【Softmax多分类 2】代码具体实现与应用（含数据集）

推荐阅读

前言