前言：关于决策树的含义这里就不详细解释了，简单来说决策树就是根据数据集的最优特征构造一棵树，再用这棵树来预测新的数据属于哪一类。决策树是一种基本的分类算法。（实际上也可以用于回归，这里不做讨论）
参考文章：机器学习实战（三）——决策树_呆呆的猫的博客-CSDN博客_决策树
数据挖掘领域十大经典算法之—C4.5算法（超详细附代码）_fuqiuai的博客-CSDN博客_c4.5

构造决策树的算法

一般构建决策树的算法有三种：ID3，C4.5，CART。此三种算法的区别在于：

ID3：特征划分基于信息增益。ID3 仅仅适用于分类问题；ID3 仅仅能够处理离散属性。
C4.5：特征划分基于信息增益比。可以处理连续值。
CART：特征划分基于基尼系数。并且CART算法只能构造出二叉树。CART 既可以用于分类问题，也可以用于回归问题。

信息增益与信息增益比

熵

简单来说，在这里熵是用来衡量数据集纯净度的。熵的值越小，代表数据集纯净度越高。反之，熵越大代表数据集越混乱。

熵的计算公式为：

$H = -\sum_{i=1}^np(x_i)log_2p(x_i)$

$x_i$为第i个分类，$p(x_i)$为选择该分类的概率。

经验熵

当上诉的$p(x_i)$（即选则某一类的概率）是由数据估计（特别是最大似然估计）得到时，此时的熵被称为经验熵。举个例子：

类别	个数
A	4
B	6

如果$p(A) = \frac 4 {10},P(B) = \frac 6 {10}$,那么此时算出的熵就是经验熵。

经验熵的公式可以写为：

$H(D) = -\sum_{k=1}^n \frac {|c_k|}{|D|}log_2\frac {|c_k|}{|D|}$

使用上式可算出例中的经验熵$H(D)$为：

$H(D) = -log_2-log_2 = 0.971 $

条件熵

条件熵$H(Y|X)$表示在已知随机变量$X$的条件下，随机变量$Y$的不确定性。

公式：

\[ \begin{split} H(Y|X) &= \sum_{i=1}^nP(x_i)H(Y|X = x_i)\\&= -\sum_{i=1}^nP(x_i)\sum_{j=1}^mP(y_i|x_i)log_2P(y_i|x_i)\\&= -\sum_{i=1}^n\sum_{j=1}^mP(x_i,y_j)log_2P(y_j|x_i) \end{split} \]

这个条件熵，可能最开始不太好理解，建议参考这篇文章，里面有详细的说明和例题，这里就不举例了。通俗理解条件熵_AI_盲的博客-CSDN博客_条件熵

经验熵对应的条件熵为经验条件熵，一般我们计算的都是经验条件熵。注：经验条件熵必须会自己手算。

特别的，令$0log_20 = 0$。

信息增益

信息增益指知道了某个条件后，事件的不确定性的下降程度。特征A对训练集D的信息增益$g(D,A)$被定义为集合D的经验熵$H(D)$与给定特征A的条件下的经验条件熵$H(D|A)$之差：

$G(D,A)=H(D)-H(D|A)$

如果一个特征的信息增益越大，说明使用这个特征划分后的样本集可以拥有更好的纯净度。所以在ID3算法中，每一轮我们会计算每个未使用特征的信息增益，然后选择信息增益最大的那个特征作为划分节点。但是这样会有个问题，假设每个属性中每种类别都只有一个样本，那这样属性信息熵就等于零，根据信息增益就无法选择出有效分类特征。

所以提出了信息增益率作为标准的C4.5算法。

信息增益率

信息增益率$GainRatio(D,A)$由信息增益$G(D,A)$和分裂信息度量$SplitInformation(D,A)$共同定义，公式如下：

$GainRatio(D,A) = \frac{G(D,A)}{SplitInformation(D,A)}$

$SplitInformation(D,A) = -\sum_{i=1}^n\frac{|S_i|}{|S|}log_2\frac{|S_i|}{S}$

也有人把信息增益率的公式写为：

$GainRatio(D,A) = \frac{G(D,A)}{H(D)}$，$H(D)$为训练集D的经验熵。

需要注意的是，增益率准则对可取值数目较少的属性所有偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

关于CART算法和基尼系数

不在这里进行说明，之后可能会单独开一篇文章。

决策树的构建

上面已经介绍了构建决策树需要用到的子模块，即经验熵的计算和最优特征的选择。接下来介绍决策树的整体构建步骤。

构建决策树的核心都是递归算法，结束递归的条件又多种，将在之后的决策树剪枝中介绍。

ID3算法

核心是在各个节点上对应信息增益准则选择特征，递归构建决策树。

具体方法：

从根结点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征。
由该特征的不同取值建立子节点，再对子结点递归地调用以上方法，构建决策树；直到达到预剪枝条件或没有特征可以选择为止。
得到一个决策树。

C4.5算法

与ID3算法的区别在于将信息增益率作为选择特征的标准。

决策树的剪枝

如果不进行剪枝，那么决策树生成算法递归地产生决策树，直到没有特征选择为止。这样生成的决策树往往会导致过拟合。过拟合在前面的文章已经解释过，这里不再进行说明。为了防止过拟合，我们需要对决策树进行剪枝。

决策树的剪枝分为预剪枝和后剪枝两大类。

预剪枝

预剪枝指在生成决策树的过程中提前停止树的生长。常用的预剪枝有以下几种：

当树到达一定深度的时候，停止树的生长。
当信息增益，增益率和基尼指数增益小于某个阈值的时候不在生长。
达到当前节点的样本数量小于某个阈值的时候。
计算每次分裂对测试集的准确性提升，当小于某个阈值，或不再提升甚至有所下降时，停止生长。

优缺点：

优点：思想简单，算法高效，采用了贪心的思想，适合大规模问题。
缺点：提前停止生长，有可能存在欠拟合的风险。

后剪枝

后剪枝是先从训练集生成一颗完整的决策树，然后自底向上的对决策树进行剪枝。后剪枝一般不常用，这里暂时不拓展。贴一个连接：西瓜书决策树预剪枝后剪枝过程详解_铁锤2号的博客-CSDN博客

缺点：耗时太长。

利用sklearn实现决策树

关于决策树的手动实现：机器学习实战（三）——决策树_呆呆的猫的博客-CSDN博客_决策树
这篇文章写的十分完整，甚至包括决策树的储存与绘图，这里就不贴手动实现的代码了，因为感觉贴了也和他的长得几乎一样？并且文章中还提到了sklearn决策树的各种参数说明，可以说是十分详尽了。不过他代码中注释写错了一些，自己跟着走一遍就看得懂了。

导入并分割数据集

数据集下载：Classifying wine varieties | Kaggle

这个数据集sklearn其实已经内置了，只需要：

import pandas as pd
from sklearn import tree
from sklearn.datasets import load_wine
wine = load_wine()
print(wine.data) 
print(wine.target) # 分类

输出：

[[1.423e+01 1.710e+00 2.430e+00 ... 1.040e+00 3.920e+00 1.065e+03]
 [1.320e+01 1.780e+00 2.140e+00 ... 1.050e+00 3.400e+00 1.050e+03]
 [1.316e+01 2.360e+00 2.670e+00 ... 1.030e+00 3.170e+00 1.185e+03]
 ...
 [1.327e+01 4.280e+00 2.260e+00 ... 5.900e-01 1.560e+00 8.350e+02]
 [1.317e+01 2.590e+00 2.370e+00 ... 6.000e-01 1.620e+00 8.400e+02]
 [1.413e+01 4.100e+00 2.740e+00 ... 6.100e-01 1.600e+00 5.600e+02]]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]

可以更直观的展示数据集：

1
2
3

# 更直观的展示
print(pd.concat([pd.DataFrame(wine.data), pd.DataFrame(wine.target)], axis=1)) # 按列拼接
print(wine.feature_names) # 特征名称

输出：

        0     1     2     3      4     5   ...    8      9     10    11      12  0 
0    14.23  1.71  2.43  15.6  127.0  2.80  ...  2.29   5.64  1.04  3.92  1065.0   0
1    13.20  1.78  2.14  11.2  100.0  2.65  ...  1.28   4.38  1.05  3.40  1050.0   0
2    13.16  2.36  2.67  18.6  101.0  2.80  ...  2.81   5.68  1.03  3.17  1185.0   0
3    14.37  1.95  2.50  16.8  113.0  3.85  ...  2.18   7.80  0.86  3.45  1480.0   0
4    13.24  2.59  2.87  21.0  118.0  2.80  ...  1.82   4.32  1.04  2.93   735.0   0
..     ...   ...   ...   ...    ...   ...  ...   ...    ...   ...   ...     ...  ..
173  13.71  5.65  2.45  20.5   95.0  1.68  ...  1.06   7.70  0.64  1.74   740.0   2
174  13.40  3.91  2.48  23.0  102.0  1.80  ...  1.41   7.30  0.70  1.56   750.0   2
175  13.27  4.28  2.26  20.0  120.0  1.59  ...  1.35  10.20  0.59  1.56   835.0   2
176  13.17  2.59  2.37  20.0  120.0  1.65  ...  1.46   9.30  0.60  1.62   840.0   2
177  14.13  4.10  2.74  24.5   96.0  2.05  ...  1.35   9.20  0.61  1.60   560.0   2

[178 rows x 14 columns]
['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']

分割数据集为训练集和测试集（7：3）

1 2	X_train,X_test,y_train,y_test = train_test_split(wine.data,wine.target,train_size=0.7) print(pd.concat([pd.DataFrame(X_train), pd.DataFrame(y_train)], axis=1))

输出：

        0     1     2     3      4     5   ...    8     9     10    11      12  0 
0    12.08  1.83  2.32  18.5   81.0  1.60  ...  1.64  2.40  1.08  2.27   480.0   1
1    11.82  1.72  1.88  19.5   86.0  2.50  ...  1.42  2.06  0.94  2.44   415.0   1
2    13.72  1.43  2.50  16.7  108.0  3.40  ...  2.04  6.80  0.89  2.87  1285.0   0
3    13.49  3.59  2.19  19.5   88.0  1.62  ...  0.88  5.70  0.81  1.82   580.0   2
4    13.05  2.05  3.22  25.0  124.0  2.63  ...  1.92  3.58  1.13  3.20   830.0   0
..     ...   ...   ...   ...    ...   ...  ...   ...   ...   ...   ...     ...  ..
119  12.42  4.43  2.73  26.5  102.0  2.20  ...  1.71  2.08  0.92  3.12   365.0   1
120  14.22  1.70  2.30  16.3  118.0  3.20  ...  2.03  6.38  0.94  3.31   970.0   0
121  13.16  2.36  2.67  18.6  101.0  2.80  ...  2.81  5.68  1.03  3.17  1185.0   0
122  11.84  2.89  2.23  18.0  112.0  1.72  ...  0.95  2.65  0.96  2.52   500.0   1
123  12.86  1.35  2.32  18.0  122.0  1.51  ...  0.94  4.10  0.76  1.29   630.0   2

[124 rows x 14 columns]

决策树算法一般不需要标准化，所以这里省去了标准化。

建立并训练决策树

sklearn并没有实现C4.5算法，所以这里用的ID3,所以要用C4.5算法还是需要手动实现。sklearn默认使用的是CART算法（基尼系数）。

1
2
3

dec_tree = tree.DecisionTreeClassifier(criterion='entropy')
# 如果criterion不填则默认使用gini系数。
dec_tree = dec_tree.fit(X_train,y_train)

测试决策树

y_predict = dec_tree.predict(X_test)
print(f"y predict value is:{y_predict}")
print(f"y ture value is:{y_test}")
f1_score = f1_score(y_test, y_predict, average='weighted')
print(f"F1-Score is {f1_score}")

输出：

y predict value is:[1 2 1 1 1 1 1 1 0 1 1 0 1 1 2 0 1 2 1 2 1 2 2 0 0 0 0 2 0 1 0 0 1 1 2 0 0
 2 0 0 1 2 0 2 1 1 0 1 0 1 0 2 1 0]
y ture value is:[1 2 1 1 1 1 1 2 0 1 1 0 0 1 2 0 0 2 1 2 1 1 2 0 0 0 0 2 0 1 0 0 1 1 2 0 0
 2 0 0 1 2 0 2 1 1 0 1 0 1 0 2 1 0]
F1-Score is 0.9266835016835017

使用Graphviz绘制决策树

下载graphviz：Download | Graphviz

配置环境变量：

pip安装graphviz：

1	!pip install graphviz -i https://pypi.tuna.tsinghua.edu.cn/simple

然后重启Pycharm，

import graphviz
feature_name = ['酒精', '苹果酸', '灰', '灰的碱性', '镁', '总酚', '类黄酮', '非黄烷类酚类', '花青素', '颜色强度', '色调', '稀释葡萄酒', '脯氨酸']
dot_data = tree.export_graphviz(dec_tree
                                , feature_names=feature_name
                                , class_names=['琴酒', '雪莉', '贝尔摩德']
                                , filled=True
                                , rounded=True
                                , fontname="Microsoft YaHei")  # 圆角
graph = graphviz.Source(dot_data)
graph.view()

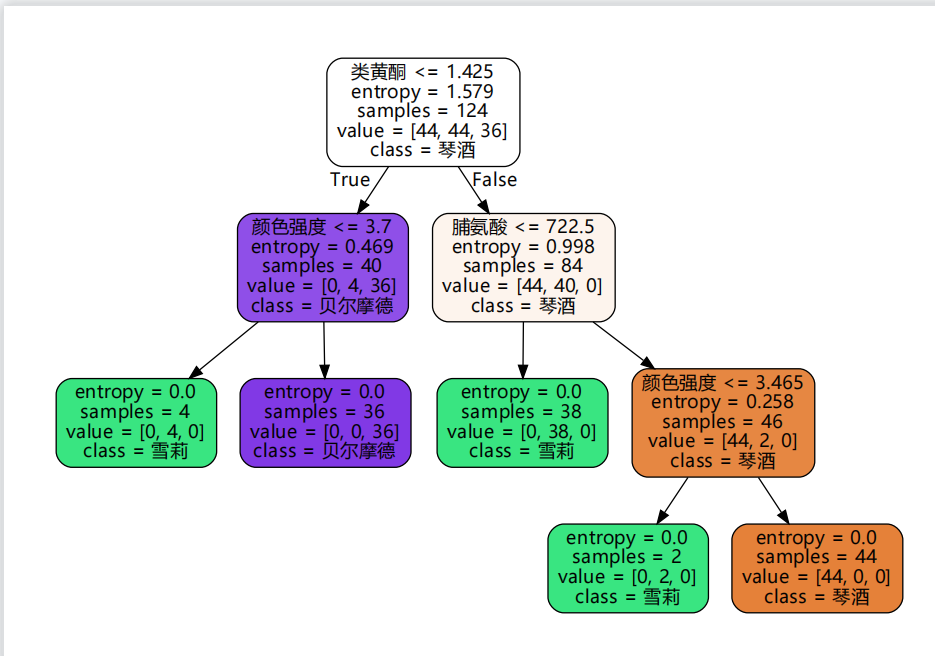
保存和读取决策树

决策树的训练过程往往很浪费时间，所以我们可以把训练好的决策树保存起来方便直接调用。这里介绍模型保存方法，不仅仅适用于决策树，而适用于所有模型。

使用pickle保存模型

存储模型：

import pickle

'''储存模型'''
def save_model(model):
    with open('train_model.pkl','wb') as f:
        pickle.dump(model,f)

新开一个py读取模型并查看模型:

import pickle
import graphviz
from sklearn import tree

'''读取模型'''
def read_model(path):
    with open(path,'rb') as f:
        model = pickle.load(f)
    return model

dec_tree = read_model('train_model.pkl')

feature_name = ['酒精', '苹果酸', '灰', '灰的碱性', '镁', '总酚', '类黄酮', '非黄烷类酚类', '花青素', '颜色强度', '色调', '稀释葡萄酒', '脯氨酸']
dot_data = tree.export_graphviz(dec_tree
                                , feature_names=feature_name
                                , class_names=['琴酒', '雪莉', '贝尔摩德']
                                , filled=True
                                , rounded=True
                                , fontname="Microsoft YaHei")  # 圆角
graph = graphviz.Source(dot_data)
graph.view()

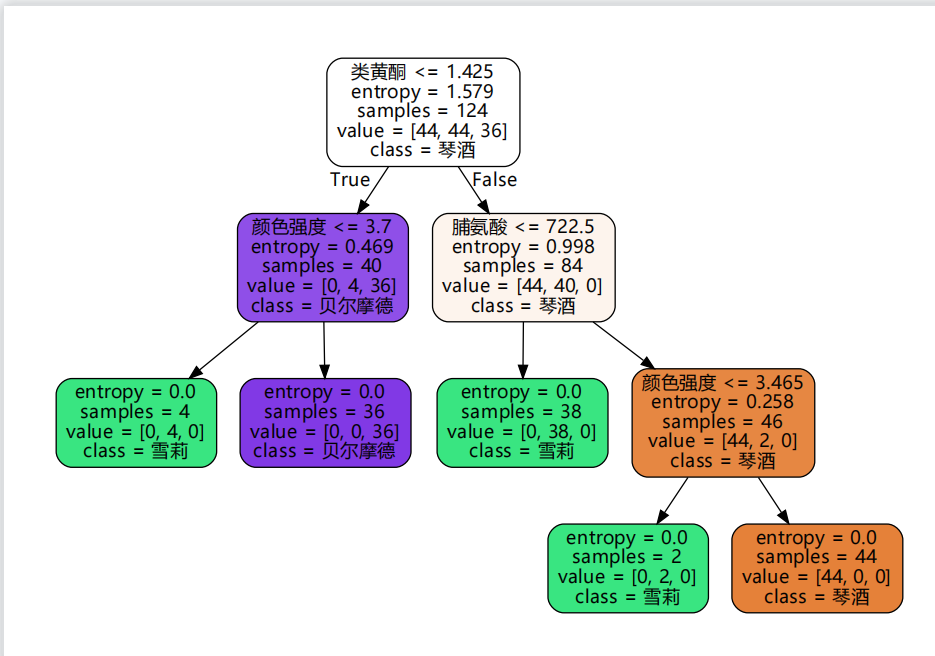
决策树的优缺点

优点：

可以可视化，易于理解
决策树几乎不需要预处理

缺点：

决策树可能会创建一棵过于复杂的树，容易过拟合，需要选择合适的剪枝策略
决策树对训练集十分敏感，哪怕训练集稍微有一点变化，也可能会产生一棵完全不同的决策树。（可以在分割训练集时把随机种子去掉，会发现每次的决策树都不一样）

最后还是贴一个C4.5的实现文章连接吧：python实现C4.5_张##的博客-CSDN博客